Stat-Ease Blog

Categories
Tips and tricks for designing statistically optimal experiments
Like the blog? Never miss a post - sign up for our blog post mailing list.
A fellow chemical engineer recently asked our StatHelp team about setting up a response surface method (RSM) process optimization aimed at establishing the boundaries of his system and finding the peak of performance. He had been going with the Stat-Ease software default of I-optimality for custom RSM designs. However, it seemed to him that this optimality “focuses more on the extremes” than modified distance or distance.
My short answer, published in our September-October 2025 DOE FAQ Alert, is that I do not completely agree that I-optimality tends to be too extreme. It actually does a lot better at putting points in the interior than D-optimality as shown in Figure 2 of "Practical Aspects for Designing Statistically Optimal Experiments." For that reason, Stat-Ease software defaults to I-optimal design for optimization and D-optimal for screening (process factorials or extreme-vertices mixture).
I also advised this engineer to keep in mind that, if users go along with the I-optimality recommended for custom RSM designs and keep the 5 lack-of-fit points added by default using a distance-based algorithm, they achieve an outstanding combination of ideally located model points plus other points that fill in the gaps.
For a more comprehensive answer, I will now illustrate via a simple two-factor case how the choice of optimality parameters in Stat-Ease software affects the layout of design points. I will finish up with a tip for creating custom RSM designs that may be more practical than ones created by the software strictly based on optimality.
An illustrative case
To explore options for optimal design, I rebuilt the two-factor multilinearly constrained “Reactive Extrusion” data provided via Stat-Ease program Help to accompany the software’s Optimal Design tutorial via three options for the criteria: I vs D vs modified distance. (Stat-Ease software offers other options, but these three provided a good array to address the user’s question.)
For my first round of designs, I specified coordinate exchange for point selection aimed at fitting a quadratic model. (The default option tries both coordinate and point exchange. Coordinate exchange usually wins out, but not always due to the random seed in the selection algorithm. I did not want to take that chance.)
As shown in Figure 1, I added 3 additional model points for increased precision and kept the default numbers of 5 each for the lack-of-fit and replicate points.
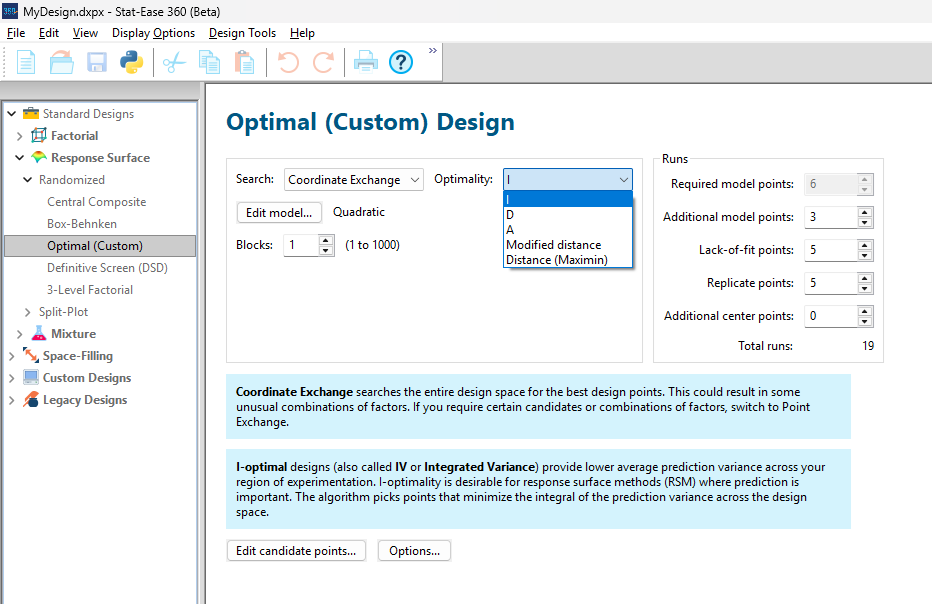
Figure 1: Set up for three alternative designs—I (default) versus D versus modified distance
As seen in Figure 2’s contour graphs produced by Stat-Ease software’s design evaluation tools for assessing standard error throughout the experimental region, the differences in point location are trivial for only two factors. (Replicated points display the number 2 next to their location.)
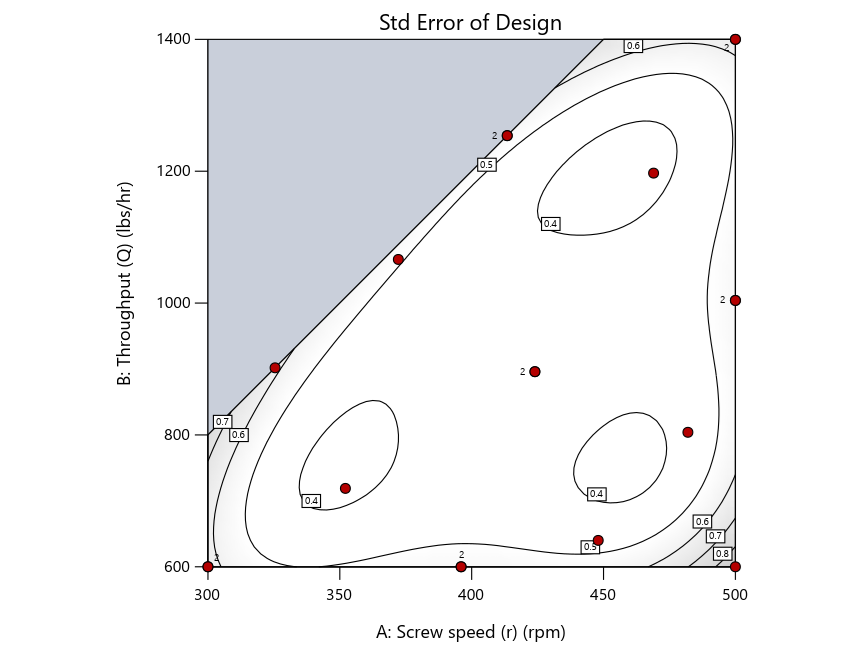
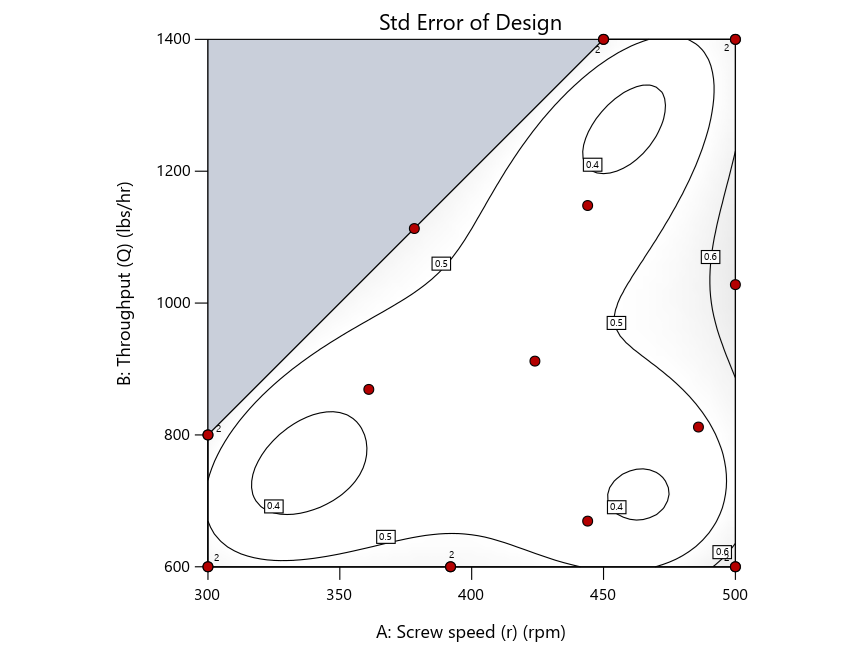
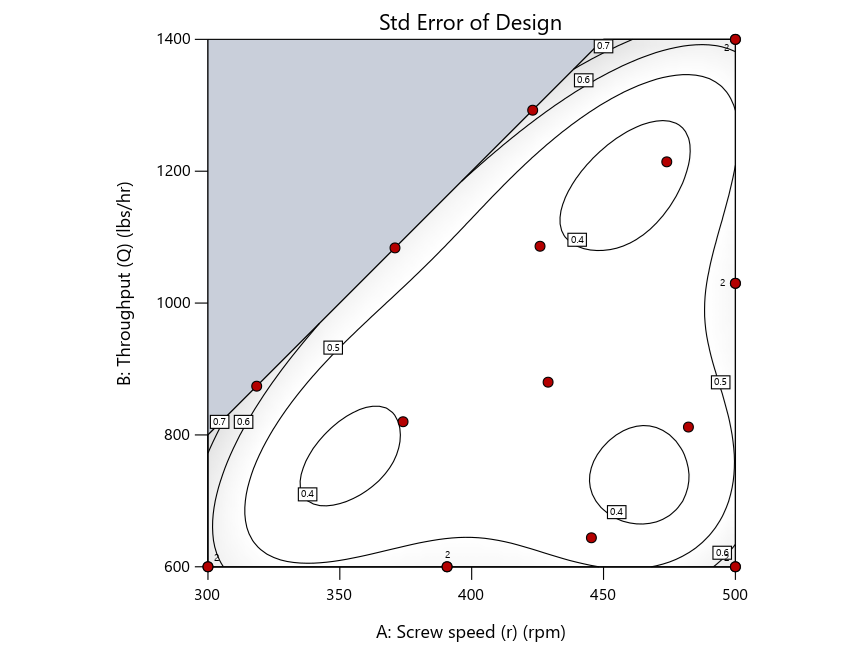
Figure 2: Designs built by I vs D vs modified distance including 5 lack-of-fit points (left to right)
Keeping in mind that, due to the random seed in our algorithm, run-settings vary when rebuilding designs, I removed the lack-of-fit points (and replicates) to create the graphs in Figure 2.
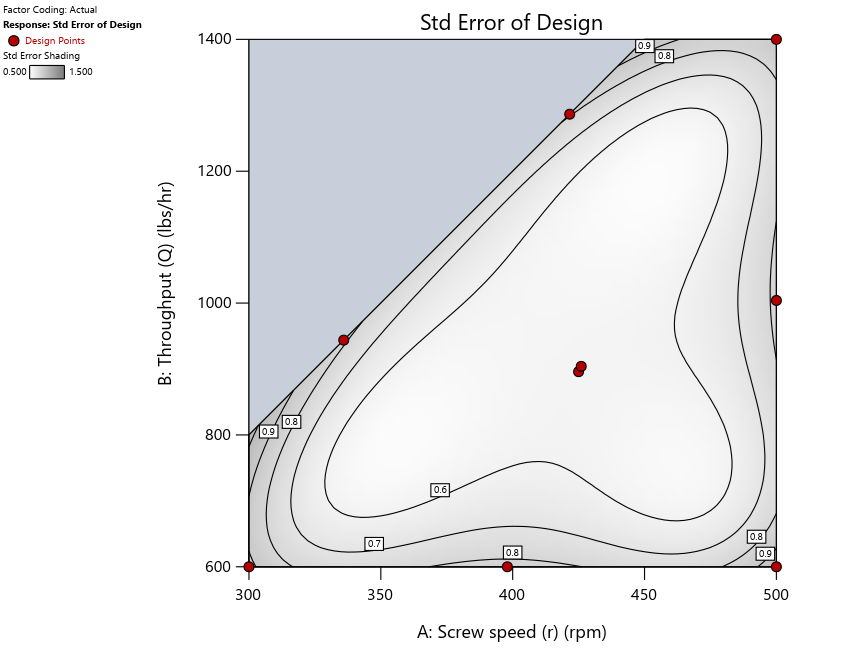
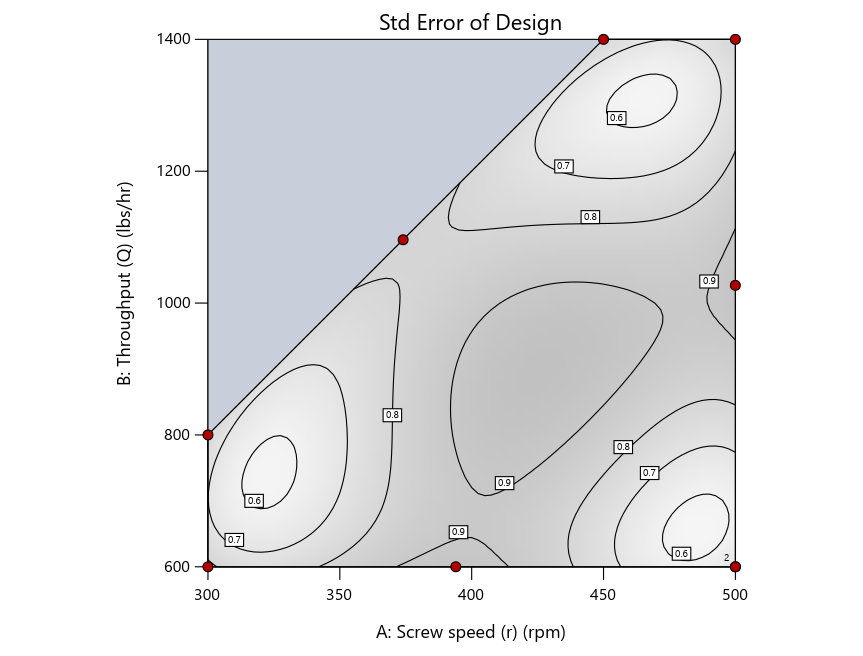
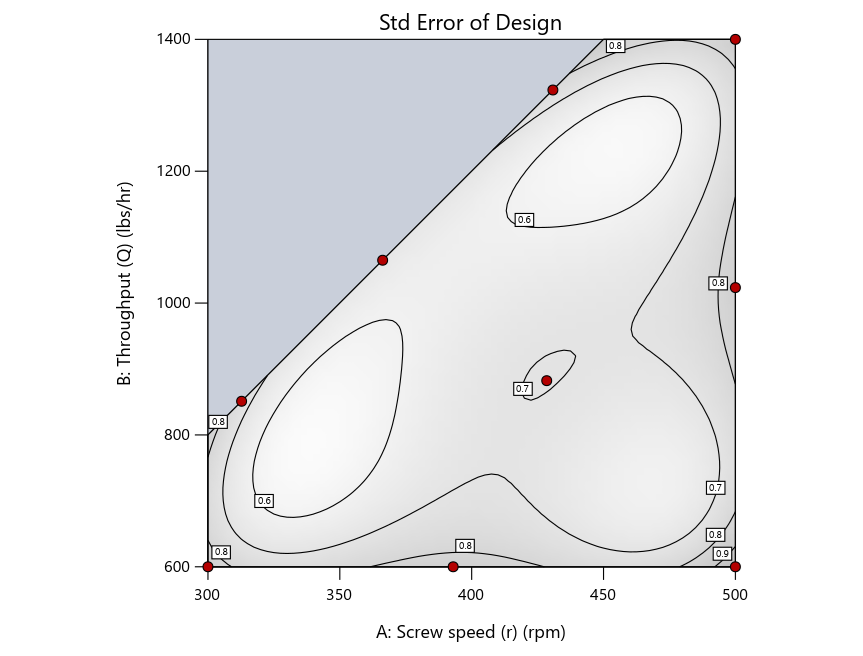
Figure 3: Designs built by I vs D vs modified distance excluding lack-of-fit points (left to right)
Now you can see that D-optimal designs put points around the outside, whereas I-optimal designs put points in the interior, and the space-filling criterion spreads the points around. Due to the lack of points in the interior, the D-optimal design in this scenario features a big increase in standard error as seen by the darker shading—a very helpful graphical feature in Stat-Ease software. It is the loser as a criterion for a custom RSM design. The I-optimal wins by providing the lowest standard error throughout the interior as indicated by the light shading. Modified distance base selection comes close to I optimal but comes up a bit short—I award it second place, but it would not bother me if a user liking a better spread of their design points make it their choice.
In conclusion, as I advised in my DOE FAQ Alert, to keep things simple, accept the Stat-Ease software custom-design defaults of I optimality with 5 lack-of-fit points included and 5 replicate points. If you need more precision, add extra model points. If the default design is too big, cut back to 3 lack-of-fit points included and 3 replicate points. When in a desperate situation requiring an absolute minimum of runs, zero out the optional points and ignore the warning that Stat-Ease software pops up (a practice that I do not generally recommend!).
A practical tip for point selection
Look closely at the I-optimal design created by coordinate exchange in Figure 3 on the left and notice that two points are placed in nearly the same location (you may need a magnifying glass to see the offset!). To avoid nonsensical run specifications like this, I prefer to force the exchange algorithm to point selection. This restricts design points to a geometrically registered candidate set, that is, the points cannot move freely to any location in the experimental region as allowed by coordinate exchange.
Figure 4 shows the location of runs for the reactive-extrusion experiment with point selection specified.
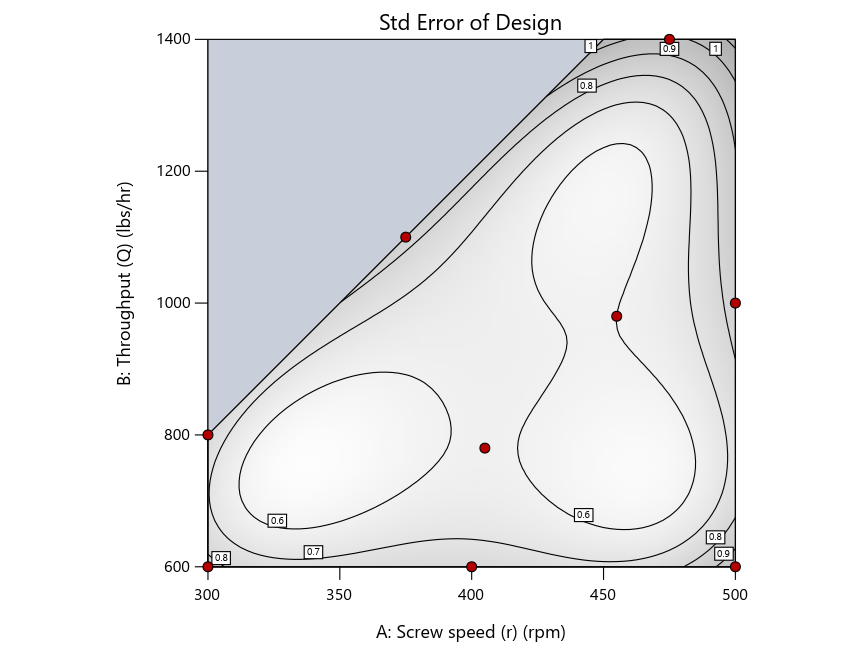
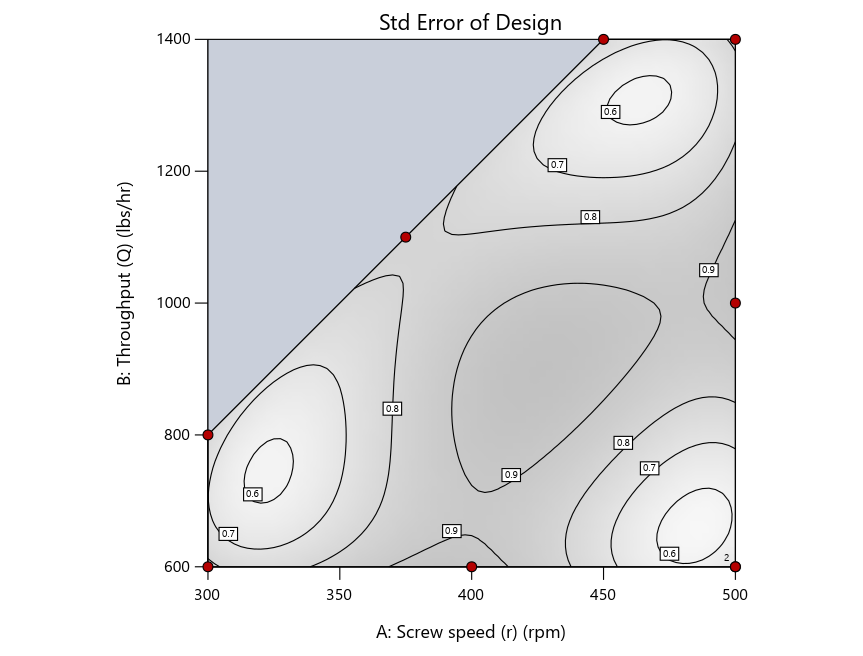
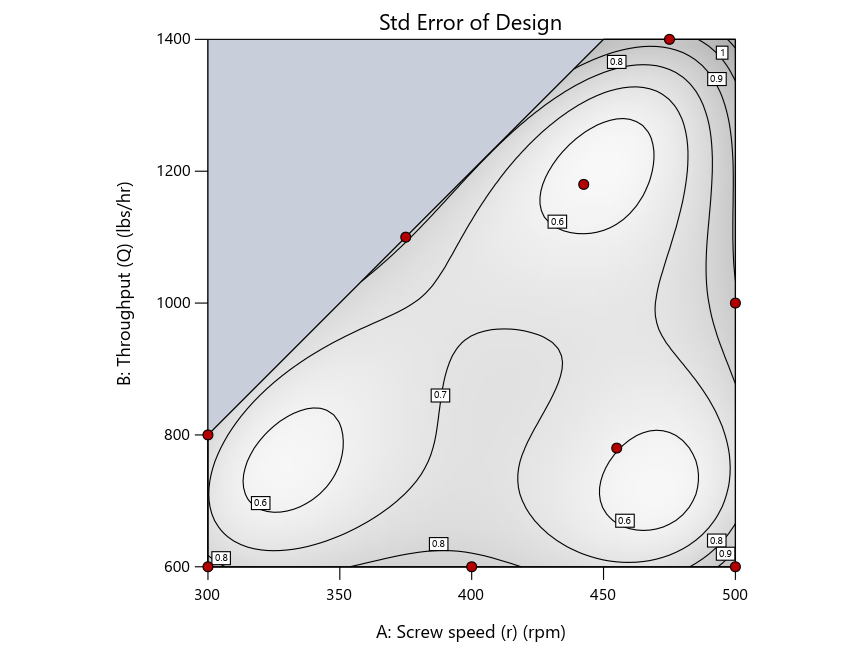
Figure 4: Designs built by I vs D vs modified distance by point exchange (left to right)
The D optimal remains a bad choice—the same as before. The edge for I optimal over modified distance narrows due to point exchange not performing quite as well for as coordinate exchange.
As an engineer with a wealth of experience doing process development, I like the point exchange because it:
- Reaches out for the ‘corners’—the vertices in the design space,
- Restricts runs to specific locations, and
- Allows users to see where they are by showing space point type on the design layout enabled via a right-click over the upper left corner.
Figures 5a and 5b illustrate this advantage of point over coordinate exchange.
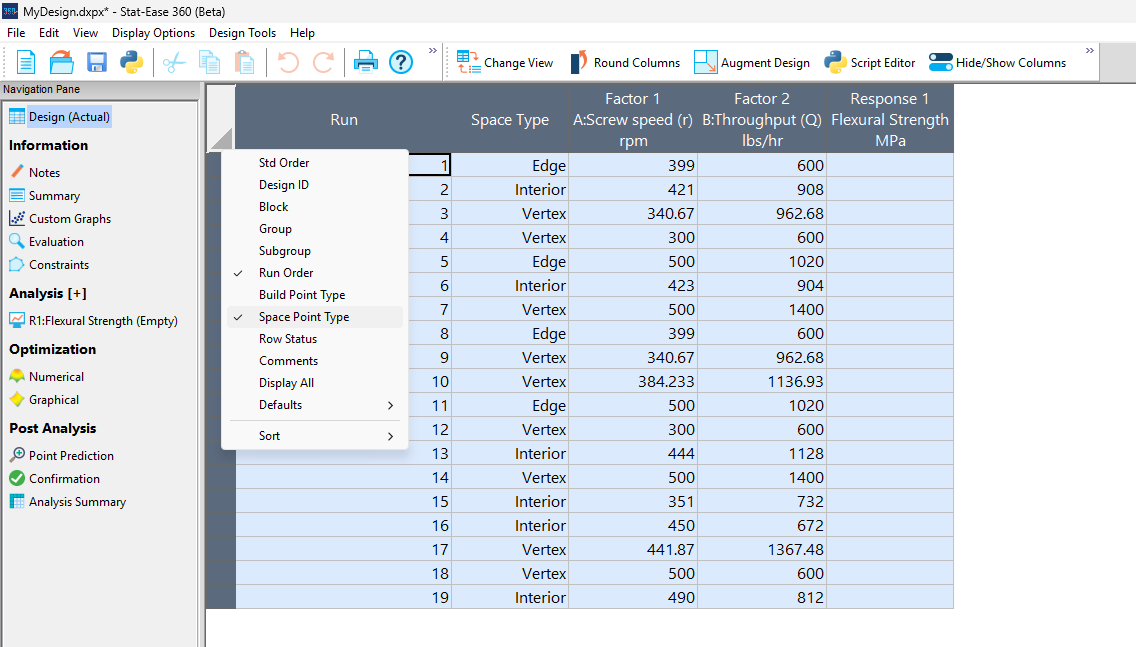
Figure 5a: Design built by coordinate exchange with Space Point Type toggled on
On the table displayed in Figure 5a for a design built by coordinate exchange, notice how points are identified as “Vertex” (good the software recognized this!), “Edge” (not very specific) and “Interior” (only somewhat helpful).
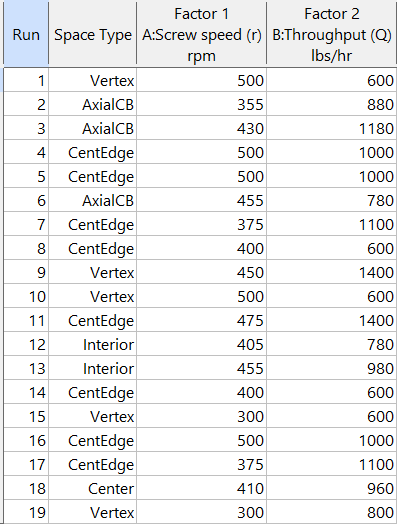
Figure 5b: Design built by point exchange with Space Point Type shown
As shown by Figure 5b, rebuilding the design via point exchange produces more meaningful identification of locations (and better registered geometrically): “Vertex” (a corner), “CentEdge” (center of edge—a good place to make a run), “Center” (another logical selection) and “Interior” (best bring up the contour graph via design evaluation to work out where these are located—click any point to identify them by run number).
Full disclosure: There is a downside to point exchange—as the number of factors increases beyond 12, the candidate set becomes excessive and thus the build takes more time than you may be willing to accept. Therefore, Stat-Ease software recommends going only with the far faster coordinate exchange. If you override this suggestion and persist with point exchange, no worries—during the build you can cancel it and switch to coordinate exchange.
Final words
A fellow chemical engineer often chastised me by saying “Mark, you are overthinking things again.” Sorry about that. If you prefer to keep things simple (and keep statisticians happy!), go with the Stat-Ease software defaults for optimal designs. Allow it to run both exchanges and choose the most optimal one, even though this will likely be the coordinate exchange. Then use the handy Round Columns tool (seen atop Figure 5a) to reduce the number of decimal places on impossibly precise settings.
Like the blog? Never miss a post - sign up for our blog post mailing list.
Salvaging a designed experiment via covariate analysis
Ideally all variables other than those included in an experiment are held constant or blocked out in a controlled fashion. However, sometimes a variable that one knows will create an important effect, such as ambient temperature or humidity, cannot be controlled. In such cases it pays to collect measurements run by run. Then the results can be analyzed with and without this ‘covariate.’
Douglas Montgomery provides a great example of analysis of covariance in section 15.3 of his textbook Design and Analysis of Experiments. It details a simple comparative experiment aimed at assessing the breaking strength in pounds of monofilament-fiber produced by three machines. The process engineer collected five samples at random from each machine, measuring the diameter of each (knowing this could affect the outcome) and testing them out. The results by machine are shown below with the diameters, measured in mils (thousandths of an inch), provided in the parentheses:
- 36 (20), 41 (25), 39 (24), 42 (25), 49 (32)
- 40 (22), 48 (28), 39 (22), 45 (30), 44 (28)
- 35 (21), 37 (23), 42 (26), 34 (21), 32 (15)
The data on diameter can be easily captured via a second response column alongside the strength measures. Montgomery reports that “there is no reason to believe that machines produce fibers of different diameters.” Therefore, creating a new factor column, copying in the diameters and regressing out its impact on strength leads to a clearer view of the differences attributed to the machines.
I will now show you the procedure for handling a covariate with Stat-Ease software. However, before doing so, analyze the experiment as planned and save this work so you can do a before and after comparison.
Figure 1 illustrates how to insert a new factor. As seen in the screenshot, I recommend this be done before the first controlled factor.

Figure 1: Inserting a new factor column for the covariate entered initially as a response
The Edit Info dialog box then appears. Type in the name and units of measure for the covariate and the actual range from low to high.

Figure 2: Detailing the covariate as a factor, including the actual range
Press “Yes” to confirm the change in actual values when the warning pops up.

Figure 3: Warning about actual values.
After the new factor column appears, the rows will be crossed out. However, when you copy over the covariate data, the software stops being so ‘cross’ (pun intended).
Press ahead to the analysis. Include only the main effect of the covariate in your model. The remainder of the terms involving controlled factors may go beyond linear if estimable. As a start, select the same terms as done before adding the covariate.
In this case, the model must be linear due to there being only one factor (machine) and it being categorical. The p-value on the effect increases from 0.0442 (significant at p<0.05) with only the machine modeled—not the diameter—to 0.1181 (not significant!) with diameter included as a covariate. The story becomes even more interesting by viewing the effects plots.

Figure 4: No covariate.

Figure 5: With covariate accounted for.
You can see that the least significant difference (LSD) bars decrease considerably from Figure 4 to Figure 5 without and with the covariate; respectively. That is a good sign—the fitting becomes far more precise by taking diameter (the covariate) into account. However, as Montgomery says, the process engineer reaches “exactly the opposite conclusion”—Machine 3 looking very weak (literally!) without considering the monofilament diameter, but when doing the covariate analysis, it becomes more closely aligned with the other two machines.
In conclusion, this case illustrates the value of recording external variables run-by-run throughout your experiment whenever possible. They then can be studied via covariate analysis for a more precise model of your factors and their effects.
This case is a bit tricky due to the question of whether fiber strength by machine differs due to them producing differing diameters, in which case this should be modeled as the primary response. A far less problematic example would be an experiment investigating the drying time of different types of paint in an uncontrolled environment. Obviously, the type of paint does not affect the temperature or humidity. By recording ambient conditions, the coating researcher could then see if they varied greatly during the experiment and, if so, include the data on these uncontrolled variables in the model via covariate analysis. That would be very wise!
PS: Joe Carriere, a fellow consultant at Stat-Ease, suggested I discuss this topic—very appealing to me as a chemical process engineer. He found the monofilament machine example, which I found very helpful (also good by seeing agreement in statistical results between our software and the one used by Montgomery).
PPS: For more advice on covariates, see this topic Help.
Tips and tools for modeling counts most precisely
In a previous Stat-Ease blog, my colleague Shari Kraber provided insights into Improving Your Predictive Model via a Response Transformation. She highlighted the most commonly used transformation: the log. As a follow up to this article, let’s delve into another transformation: the square root, which deals nicely with count data such as imperfections. Counts follow the Poisson distribution, where the standard deviation is a function of the mean. This is not normal, which can invalidate ordinary-least-square (OLS) regression analysis. An alternative modeling tool, called Poisson regression (PR) provides a more precise way to deal with count data. However, to keep it simple statistically (KISS), I prefer the better-known methods of OLS with application of the square root transformation as a work-around.
When Stat-Ease software first introduced PR, I gave it a go via a design of experiment (DOE) on making microwave popcorn. In prior DOEs on this tasty treat I worked at reducing the weight of off-putting unpopped kernels (UPKs). However, I became a victim of my own success by reducing UPKs to a point where my kitchen scale could not provide adequate precision.
With the tools of PR in hand, I shifted my focus to a count of the UPKs to test out a new cell-phone app called Popcorn Expert. It listens to the “pops” and via the “latest machine learning achievements” signals users to turn off their microwave at the ideal moment that maximizes yield before they burn their snack. I set up a DOE to compare this app against two optional popcorn settings on my General Electric Spacemaker™ microwave: standard (“GE”) and extended (“GE++”). As an additional factor, I looked at preheating the microwave with a glass of water for 1 minute—widely publicized on the internet to be the secret to success.
Table 1 lays out my results from a replicated full factorial of the six combinations done in random order (shown in parentheses). Due to a few mistakes following the software’s plan (oops!), I added a few more runs along the way, increasing the number from 12 to 14. All of the popcorn produced tasted great, but as you can see, the yield varied severalfold.
| A: | B: | UPKs | ||
|---|---|---|---|---|
| Preheat | Timing | Rep 1 | Rep 2 | Rep 3 |
| No | GE | 41 (2) | 92 (4) | |
| No | GE++ | 23 (6) | 32 (12) | 34 (13) |
| No | App | 28 (1) | 50 (8) | 43 (11) |
| Yes | GE | 70 (5) | 62 (14) | |
| Yes | GE++ | 35 (7) | 51 (10) | |
| Yes | App | 50 (3) | 40 (9) |
I then analyzed the results via OLS with and without a square root transformation, and then advanced to the more sophisticated Poisson regression. In this case, PR prevailed: It revealed an interaction, displayed in Figure 1, that did not emerge from the OLS models.

Figure 1: Interaction of the two factors—preheat and timing method
Going to the extended popcorn timing (GE++) on my Spacemaker makes time-wasting preheating unnecessary—actually producing a significant reduction in UPKs. Good to know!
By the way, the app worked very well, but my results showed that I do not need my cell phone to maximize the yield of tasty popcorn.
To succeed in experiments on counts, they must be:
- discrete whole numbers with no upper bound
- kept with within over a fixed area of opportunity
- not be zero very often—avoid this by setting your area of opportunity (sample size) large enough to gather 20 counts or more per run on average.
For more details on the various approaches I’ve outlined above, view my presentation on Making the Most from Measuring Counts at the Stat-Ease YouTube Channel.
The Importance of Center Points in Central Composite Designs
A central composite design (CCD) is a type of response surface design that will give you very good predictions in the middle of the design space. Many people ask how many center points (CPs) they need to put into a CCD. The number of CPs chosen (typically 5 or 6) influences how the design functions.
Two things need to be considered when choosing the number of CPs in a central composite design:
1) Replicated center points are used to estimate pure error for the lack of fit test. Lack of fit indicates how well the model you have chosen fits the data. With fewer than five or six replicates, the lack of fit test has very low power. You can compare the critical F-values (with a 5% risk level) for a three-factor CCD with 6 center points, versus a design with 3 center points. The 6 center point design will require a critical F-value for lack of fit of 5.05, while the 3 center point design uses a critical F-value of 19.30. This means that the design with only 3 center points is less likely to show a significant lack of fit, even if it is there, making the test almost meaningless.
TIP: True “replicates” are runs that are performed at random intervals during the experiment. It is very important that they capture the true normal process variation! Do not run all the center points grouped together as then most likely their variation will underestimate the real process variation.
2) The default number of center points provides near uniform precision designs. This means that the prediction error inside a sphere that has a radius equal to the ±1 levels is nearly uniform. Thus, your predictions in this region (±1) are equally good. Too few center points inflate the error in the region you are most interested in. This effect (a “bump” in the middle of the graph) can be seen by viewing the standard error plot, as shown in Figures 1 & 2 below. (To see this graph, click on Design Evaluation, Graph and then View, 3D Surface after setting up a design.)

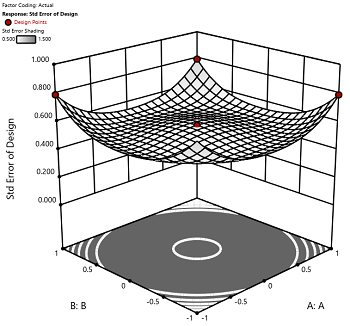
Figure 1 (left): CCD with the 6 center points (5-6 recommended). Figure 2 (right): CCD with only 3 center points. Notice the jump in standard error at the center of figure 2.
Ask yourself this—where do you want the best predictions? Most likely at the middle of the design space. Reducing the number of center points away from the default will substantially damage the prediction capability here! Although it can seem tedious to run all of these replicates, the number of center points does ensure that the analysis of the design can be done well, and that the design is statistically sound.
Augmenting One-Factor-at-a-Time Data to Build a DOE
I am often asked if the results from one-factor-at-a-time (OFAT) studies can be used as a basis for a designed experiment. They can! This augmentation starts by picturing how the current data is laid out, and then adding runs to fill out either a factorial or response surface design space.
One way of testing multiple factors is to choose a starting point and then change the factor level in the direction of interest (Figure 1 – green dots). This is often done one variable at a time “to keep things simple”. This data can confirm an improvement in the response when any of the factors are changed individually. However, it does not tell you if making changes to multiple factors at the same time will improve the response due to synergistic interactions. With today’s complex processes, the one-factor-at-a-time experiment is likely to provide insufficient information.

Figure 1: OFAT
The experimenter can augment the existing data by extending a factorial box/cube from the OFAT runs and completing the design by running the corner combinations of the factor levels (Figure 2 – blue dots). When analyzing this data together, the interactions become clear, and the design space is more fully explored.

Figure 2: Fill out to factorial region
In other cases, OFAT studies may be done by taking a standard process condition as a starting point and then testing factors at new levels both lower and higher than the standard condition (see Figure 3). This data can estimate linear and nonlinear effects of changing each factor individually. Again, it cannot estimate any interactions between the factors. This means that if the process optimum is anywhere other than exactly on the lines, it cannot be predicted. Data that more fully covers the design space is required.

Figure 3: OFAT
A face-centered central composite design (CCD)—a response surface method (RSM)—has factorial (corner) points that define the region of interest (see Figure 4 – added blue dots). These points are used to estimate the linear and the interaction effects for the factors. The center point and mid points of the edges are used to estimate nonlinear (squared) terms.

Figure 4: Face-Centered CCD
If an experimenter has completed the OFAT portion of the design, they can augment the existing data by adding the corner points and then analyzing as a full response surface design. This set of data can now estimate up to the full quadratic polynomial. There will likely be extra points from the original OFAT runs, which although not needed for model estimation, do help reduce the standard error of the predictions.
Running a statistically designed experiment from the start will reduce the overall experimental resources. But it is good to recognize that existing data can be augmented to gain valuable insights!
Learn more about design augmentation at the January webinar: The Art of Augmentation – Adding Runs to Existing Designs.
